2019国考行测数量关系备考技巧之整除思想

整除思想一直都是历年国考数量关系必考的内容。并且，一般在国考的数量关系题目中都有2-4道题目可以利用整除的解题方式去选择或者排除部分选项，进而实现提高解题正确率的目的。对于大部分学员而言，合理正确的使用整除特性能够在很大程度简化运算，排除选项最终得出最后的答案。

对于学员而言，需要掌握的关于整除的内容主要包括：1、认识到利用整除思想解题带来的便利。2、熟练掌握常见数的整除特性，并且能够准确判断。3、利用整除关系解决一些含不可拆分量的运用题。4、利用整除的解题思路简化不定方程的解法。

一、介绍整除的意义以及核心

整除思想倾向于运用整除的特性去判断和排除选项，所以在很多时候并不是把这道题目按照正常的计算方法算出答案。而更多的时候是利用这个关系排除掉题目的选项。会通过例题来让同学们体会整除思想的内涵。

例题：

一些员工在某工厂车间工作，如果有4名女员工离开车间，在剩余的员工中，女员工人数占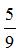;如果有4名男员工离开车间，在剩余的员工中，男员工人数占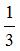。原来在车间工作的员工有( )名。

A、36 B、40 C、48 D、72

解析：总人数-4能被9整除。

通过这道题目让学员明白，整除特性解题所带来的便利以及整除思想在数量关系的使用方法。

二、常见数的整除特性

此部分主要是介绍一些常见数的整除特性，能够让学员更好的认识，并且能够熟练掌握常见数(比如2、5、3、9、11等)的整除特性，进而能够更好的使用并通过练习题的方式强化学员的理解。

三、整除的运用环境

通过前面两个部分的学习，学员基本上已经能够掌握常见数的整除特性。在这里中公教育专门提出，在考试过程中并不会像前面题目那样直接告诉你整除，而更多的时候是判断，所以这里主要是通过讲解整除的运用环境，将整除的运用环境扩大，并且辅以练习题进行提升。主要是以国考真题为主进行讲解

例如：某公司有员工830人，今年男员工人数比去年减少6%，女员工人数比去年增加5%，员工总数比去年增加3人。问今年男员工有多少人?

A、329 B、350 C、371 D、504

解析：今年男员工：去年男员工=94%=94：100=47：50.进而得出今年男员工为47的倍数。

四、整除特性在不定方程的运用

在做数量关系的时候，很多学生比较习惯于利用方程来解题，所以经常会碰到解不定方程的时候，这里可以利用整除的一些基本特性，使得不定方程的可能性变少，达到减少讨论可能性的目的。举例子： 2X+3Y=60 2X+5Y=59 (X、Y为整数)

通过这两个简单的例子让学员明白在解决不定方程的时候，经常可以利用前面讲的整除特性简化计算过程。然后再通过几道真题让学员自己训练解题的技巧。

总之。对于整除思想，它既是一个必考的思想，也是一个相对来说比较简单的数学思想，所以在课堂上中公教育务必保证每一个学员都能够掌握并且熟练运用。