行测技巧：数量关系之巧解利润问题（2）

方法2：特值

应用环境：所求问题为比值关系且对应量均未知

例3：某商品按原价出售，每件商品可获得50%利润，后来按照原价的80%出售，结果每天售出的件数比降价前增加了2倍，那么后来每天销售这种商品所赚取的利润是原来的多少倍?

A0.8 B1.2 C1.5 D1.8

题目关键：所求结果为倍数为一个比值问题且对应的前后利润额未知

利润问题存在比较时解题小技巧：列表

中公解析：

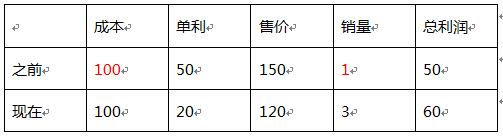
表格中标红之处为所设的特值，围绕所设特值尽可能整及尽可能小的原则可将商品成本设为100，之前销量设为1，其他变量可根据题干信息进行逻辑推导最终可知总利润前后为1.2倍

方法3：方程+特值

例4：一种商品今年的成本比去年下降了10%，但是售价没变，因此利润上升了20%，则这种商品今年的售价是成本几倍?

A、4∕3 B、5∕3 C、5∕4 D、7∕3

题目关键：所求为倍数是一个比值关系

售价未变存在等量关系

中公解析：

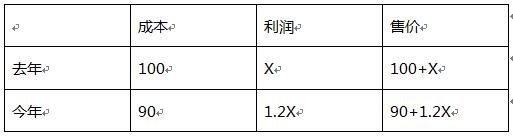
根据等量关系售价未变，可得100+X=90+1.2X，则X=50，因此今年的售价为150元

所求倍数为150∕90即5∕3

利润问题难度适中，适合在考场中选用针对性的方法进行解决，当然利润问题解题方法还包括十字交叉法，因为十字交叉法能解决的问题都可以用特值进行计算，因此在本文中就不再提及十字交叉法解决利润问题的内容，希望通过本文考生能够熟练利润问题的相关概念、公式以及解题方法。